Variable types
Before getting into why Arduino math does not work, I need to cover a brief explanation on variable types. If you know the difference between integer and float, you can skip down to the next section. Computers have a difficult time with decimal numbers. Binary representations work great for integers like 1,2,3,4,5, etc. Decimal points, however, add complexity to the situation. For that reason, numeric variable types are known as “integer” or “floating point.” Integer types can only handle, well, integers, while floating point can hold decimal numbers.All of the examples here are using an Arduino Uno. That board is based on the Microchip ATmega328p.
#1 Long Arduino delay()s don’t work
Skipping right passed delay() vs. millis(), a common action is doing a delay that lasts hours or days. This problem seems to come up with projects like sprinklers or aquariums. Instead of doing the math ahead of time, you might try letting the computer do the work for you.
// 1000 ms, 60 sec, 60 min, 24, hours, 14 days
unsigned long wait = 1000 * 60 * 60 * 24 * 14;
Serial.print("wait = ");
Serial.println(wait);
// Prints wait = 2048
// 1000 ms, 60 sec, 60 min, 24, hours, 14 days
unsigned long wait = 1000UL * 60 * 60 * 24 * 14;
Serial.print("wait = ");
Serial.println(wait);
// Prints: wait = 1209600000
unsigned long wait = 1000 * 60 * 60 * 24 * 14UL;
// Prints: wait = 329728
warning: integer overflow in expression [-Woverflow]
unsigned long wait = 1000 * 60 * 60 * 24 * 14;
#2 Why does Arduino division result in a zero?
Look at this code example. What do you expect the serial monitor to print?
float example = 3 / 5 * 2;
Serial.print("example = ");
Serial.println(example);
// Prints: example = 0.00
float example = 3.0 / 5.0 * 2.0;
Serial.print("example = ");
Serial.println(example);
// Prints: example = 1.20
#3 Arduino math does not Round
Starting off, here is the same math operation from above but with “example” declared as an integer instead of a float.
int example = 3.0 / 5 * 2;
Serial.print("example = ");
Serial.println(example);
// Prints: example = 1
int example = 5.0 / 3;
Serial.print("example = ");
Serial.println(example);
// Prints: example = 1
#4 Arduino’s float Precision
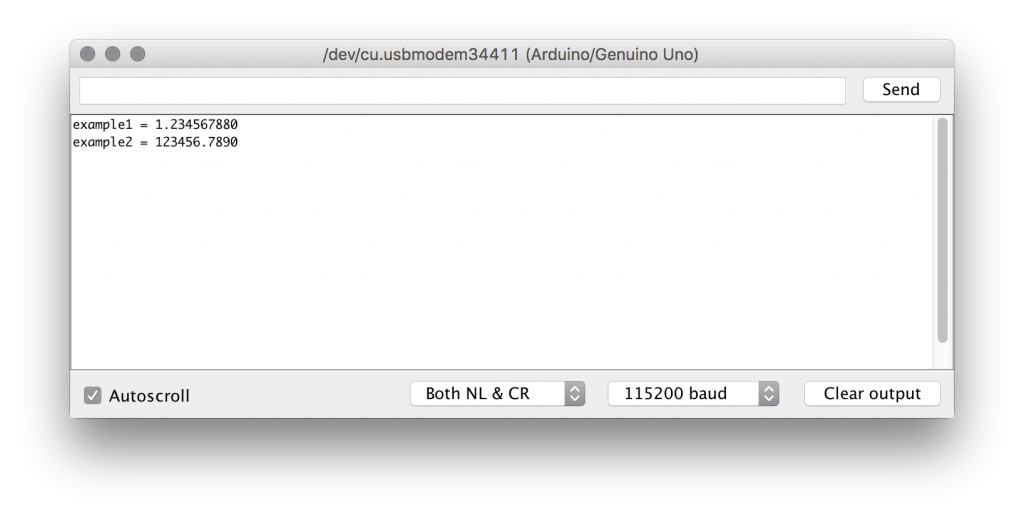
Floating point variables mean that the decimal point can float around. The precision of the number is limited to a certain number of digits. That is not the same as saying a certain number of decimals. In the case of 8-bit AVR Arduino boards, the float type is 32-bits which makes the limit 6 or 7 digits.
float example1 = 1.23456789;
float example2 = 123456.789;
Serial.print("example1 = ");
Serial.println(example1,9);
Serial.print("example2 = ");
Serial.println(example2,4);
// Prints:
// example1 = 1.234567880
// example2 = 123456.7890
#5 Order of operations
I do not want to turn this into a comment-bait Facebook post. C does have a defined operator preference. Basic operators occur in the order of Multiplication and division, then addition and subtraction. Check this reference for a complete list of operator precedence. Parenthesis, of course, is calculated first. Based on what you learned in this post and knowing there is a specific order of operations, what value does this code generate? The answer may shock you!
int example = 3 * ((5 + 2) / 4) - 1;
Serial.print("example = ");
Serial.println(example);
What Arduino or C-related math ‘issues’ have you run into wiht your code?





18 Comments
Great tips! I think I’ve covered all the bases but still having issues with a MKR WI-FI 1010. I have functions to calculate dew point and altimeter settings using all doubles (same as float on this device). Each function works as expected when used alone, but when I use them together along with several other double variables, most of them become corrupted, even variables that are not used in either function. Any ideas?
Without seeing code, no.
I was getting seconds overflows on my thermostat code that tracks how long the AC was ON, minutes was OK, until… I came across your post … problem solved by simply adding UL, how nice , ah? Thanks a lot. Stay safe , Pal!
Great ant short, thanks 🙂
Hello All,
I have reading temperature (T), pressure (P), and humidity (H) from BME280 sensors. The readings are 29.36 Deg. Celsius, 991.92 hPa, and 63.77%, respectively. I want to compute a heat index with the formula:
HI = (103.6103 – 0.1707*P + 2.3614*T+ 0.623*H).
The syntax is as below.
float P, T, H;
float HI = (103.6103 – 0.1707*P + 2.3614*T + 0.623*H);
sprintf( HI_a, “%02u.%02u”, (int)HI, (int)(HI* 100) % 100);
Serial.println(HI_a);
From calculator dengan result is 43.6941. However the reading from the serial monitor of Arduino is 88816.34. I want the result is 43.68 (2 digits after comma). What the wrong with the data type or coding? Please help. Thank you very much.
I have trying to figure why my code was failing for several days due to the order of operations of my integer math. I multiplied an Unsigned Integer variable by 1000, but the original order appeared to cause the Arduino to lock up.
Then, per your article, reversed the order of operaions and changed the 1000 to 1000UL, now the code works.
Thanks A Bunch!
I have this function
[arduino firstline=”1″]
float Calculator (unsigned long p)
{return p / 1600;}
[/arduino]
when i passing value 159999999 from loop function into it i got 99999.00 printed into serial monitor
In this case ‘p’ is a unsigned long, which is divided by 1600 (a int, implicitly converted to long) and then the result is casted to float. This is the reason you get 99999 as float.
What you probably want is casting p to a double and perform the division. Something like
[arduino firstline=”1″]
double calculator_double(unsigned long p) {
return (double)p / 1600;
}
[/arduino]
As you can see, I am using double as return value instead of a float, and there is a reason for that: you cannot represent 159999999 with a float without losing precision. If you try to print the result of the conversion to float, you will get 160000000. Using double you can obtain a more precise result, but you need to use a double as return type, otherwise you still lose precision obtaining 100000 instead of 99999.999375.
Only on platforms that support a double. AVR (and most 8-bit processors) do not support a double. A float and double have the same precision.
Hello James,
I’ve got a dum problem with simple addition.
Using float variables my math operation is
Dis = Dis + D;
It works fine until the results gets higher than 100.00. After that, only results bigger than 1.0 gets added.
Tha’s one thing. The main issue is when the result gets higher than 1000.00. It simply returns to 500.00
I don’t know if the size of the results is limited to this 5 digits. I tried long, short, byte, but that doesn’t seem to solve it.
I did an upgrade at my upcoming math, adding the .0 to all my constants, but no progress.
I’m using an arduino UNO, and my program is a GPS Tracker, that calculate the live distance ante avarage speed.
Thank you.
A float should get at least 6 digits of precision. You might try posting the code to something like pastebin for others to look at. There might be a non-obvious issue.
Loved this! It is always good to know what you are doing with different data types, you are giving very good hints! Just a small criticism: in your example with floating points, you are doing the operation using double precision — for instance 3.0 / 5.0 * 2.0 is different from 3.0f / 5.0f * 2.0f. Nevertheless, these operation will be almost surely evaluated at compile time, so it is generally difficult to get some observable differences between the two ways of writing the code.
Oh, just for you curiosity (maybe you are already aware of that): give a look to the Rust programming language, it is becoming bigger every day in the embedded world. The big downside for what you generally do is that the AVR support is actually… meh.
I forgot that .0 was actually a double. Of course in the realm of avr-gcc that does not matter, but a good point to know. Thank you for clarifying.
Thank you for the heads-up. I am working on some stuff with a tentative title of “beyond Arduino.” Currently I am learning the MSP430, next on my list is the STM32, and eventually ARM. From the quick look I did, I might include a look at Rust in that series.
Great article! Regarding #5, multiplication & division have the *same* precedence, in order from left to right, just as addition and subtraction have the same precedence in order from left to right. An example, (4 / 2 * 2) would equal 1 if multiplication had a higher precedence, but is actually 4 as precedence is the same and is read left to right.
Keep up the awesome blog!
Thanks. Good catch.
This is about Tau: What is your position on tau? I like it and try to use it now. Please give us your thoughts.
About your last example. I thought it should print “example = 2”. Then I looked again and realised it will not compile, because “Int” is not a defined type. When I fixed the compile problem, it did as I expected.
Thanks, fixed.